Table of Contents
The Objective Transforming the Target Variable
There are three problems that can occur in a machine learning project that we can tackle by transforming the target variable:
1) Improve the results of a machine learning model when the target variable is skewed.
2) Reduce the impact of outliers in the target variable
3) Using the mean absolute error (MAE) for an algorithm that only minimizes the mean squared error (MSE)
In the next part of this article, we dive a little deeper into all three points.
During the article, you will see some transformations that we are using. If you are more deeply interested in different transformations then you can also visit the article that is dedicated to transformations of features in general.
Improve the Results of a Machine Learning Model when the Target Variable is Skewed
A skewed distribution of the target variable means that the distribution differs from the normal distribution, also known as the Gaussian distribution. The normal distribution is a symmetrical bell-shaped distribution that is characterized by its mean and standard deviation.
Machine learning algorithms that are based on statistics like linear regression can be applied with greater confidence when the distribution of the target variable follows the normal distribution as much as possible. Therefore a possibility to achieve better performance and more accurate predictions is to transform the target variable to a more Gaussian distribution.
The following plot shows an original distribution of the target variable that is positively skewed (the measured skewness is positive). After applying the log transformation the distribution gets negatively skewed (skewness is negative) but with a much lower value for the skewness. Therefore the distribution is more normal. Applying the Box-Cox transformation we achieve the most normal distribution with a skewness of -0.01.
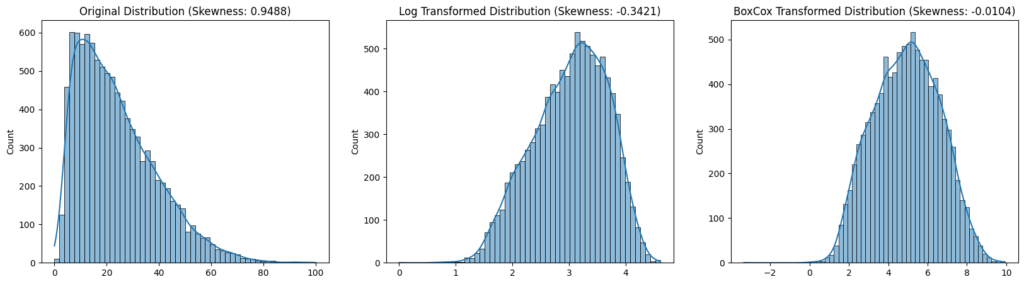
To improve the results of the machine learning model I would suggest applying the Box-Cox transformation to the target variable. The complete program code for the transformations and also for additional transformations is available at the following Google Colab
Other machine learning algorithms like tree-based models or neural networks work well with any data even when data is not normally distributed.
Reduce the Impact of Outliers
Transforming the target variable reduces the impact of outliers because the distribution changes with the transformation. Outliers for example at the extreme end of the distribution can affect the mean and standard deviation of the data, making it harder to build an accurate model. By transforming the target variable, we can change the distribution of the data so that the outliers are less extreme or have less influence on the overall distribution.
Additionally, some transformations, such as the square root or log transformation, can be particularly effective at reducing the impact of outliers because they tend to compress the extreme values in the distribution.
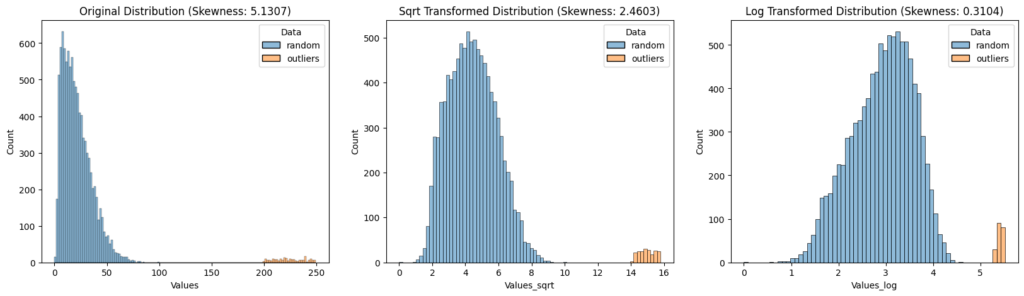
The following picture shows the distribution with outliers for the original dataset and after applying the square root transformation and log transformation. From the comparison of the skewness, you see that after the transformations the distributions are more like a Gaussian distribution, and the influence of the outliers is reduced as the difference between the outliers and the mean of the overall dataset is reduced.
Using the MAE for a Machine Learning Algorithm that only Minimizes the MSE
The transformation of the target variable does also influence the error function that you are using in a machine-learning project and can trick a machine-learning algorithm to use an error function that is not supported. For example, if the regression model only allows minimizing the MSE, we can log-transform the target variable and are close to the solution when we would use the MAE error measure. (MSE + log-transform ~ MAE)
The Easiest Way to Transform the Target Variable
After you learned the main objectives to transform the target variable, I will show you in this section different ways how to transform the target variable in Python.
To give you a little sneak peek, the easiest way to transform the target variable is to use the sklearn TransformedTargetRegressor function.
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import HuberRegressor
from sklearn.model_selection import cross_val_score
# create a pipeline that standardizes the data before using the HuberRegressor
pipeline = Pipeline(steps=[
('scaler', StandardScaler()),
('regressor', HuberRegressor())
])
# use TransformedTargetRegressor to log transform the target variable
# and calculate the rmse of all cv runs
rmse_log = np.sqrt(
-cross_val_score(
TransformedTargetRegressor(
regressor=pipeline,
func=np.log,
inverse_func=np.exp
),
X, y,
cv=5,
scoring="neg_mean_squared_error",
n_jobs=-1
)
)In the following end-to-end example, you see three different ways to compute the RMSE with cross-validation for an example dataset:
1) Calculate the RMSE of all cv runs without any transformation.
2) Only use the log-transformed target variable and calculate the RMSE of all cv runs.
3) Use TransformedTargetRegressor to log transform the target variable and calculate the RMSE of all cv runs.
- RMSE of run without transformation: [52.12826305 55.59135539 57.49187307 55.25159682 53.97513891]
- RMSE of run with only log transforming y: [0.4266049 0.40561625 0.43106019 0.39170138 0.40330288]
- RMSE of run with log transforming and retransforming y: [51.72329989 57.02066486 57.56083704 56.23000048 55.03754777]
When we compare the RMSE in the three different ways we see that when you only transform the target variable (2), you are not able to compare the errors of different runs (1), for example with different parameters to find the best parameter combination or to test if transforming the target variable improves the results.
Only if you use the TransformedTargetRegressor with the transformer function and inverse transformer function (3), the results of the cross-validation have the same scale compared to the results when no transformer is applied (1).
Read my latest articles:
