Find Outlier in Datasets using the Interquartile Range Method

The interquartile range method is my preferred method to identify outliers because the method itself is easy to understand and I created two functions that can be applied to every pandas DataFrame to create a little PDF report of all numeric features in your dataset.

The interquartile range method uses the 5-th and 95-percentile to calculate a lower and upper value where all values lower than the lower value and all values higher than the upper value are declared as outliers. You can also change the percentiles to your objective.

Read the Boston House Price Dataset

The first part of the Jupyter notebook is to import all the libraries that we use in this article and also read the dataset that we use to find the outliers. As example dataset I use the Boston house prices dataset that you can find on the Kaggle website. Because outlier are only present in the numeric features of the dataset, we also create a list where all numeric features are stored in.

import pandas as pd
import numpy as np
import os
import seaborn as sns
import matplotlib.pyplot as plt

df = pd.read_csv(
    filepath_or_buffer = '../train_bostonhouseprices.csv',
    index_col = "Id"
)

# create a list of all numeric features
numeric_col = list(df.describe())

Find Outlier and Save Histograms

The fist function, called outlier_interquartileRangeMethod, that I created finds the outliers using the interquartile range method and create a histogram for each numeric feature that shows the samples that are not declared as outliers and also the outliers. Because the function calculates the outliers for each feature separated, we use a for loop to loop over each feature in the numeric feature list and apply the function to this feature. The following program code shows the outlier_interquartileRangeMethod as well as the for loop.

def outlier_interquartileRangeMethod(df, col, save_histogram=False):
    print(col)
    
    df = df[[col]].dropna(axis='index')
    df['outlier'] = 'no outlier'
    
    q5, q95 = np.percentile(df[col], 5), np.percentile(df[col], 95)
    print("Quartile5: {:.2f} | Quartile95: {:.2f}".format(q5, q95))

    v_iqr = q95-q5
    print("iqr: {:.2f}".format(v_iqr))

    v_cut_off = v_iqr*1.5
    v_lower, v_upper = q5-v_cut_off, q95+v_cut_off
    print("CtOff: {:.2f}".format(v_cut_off))
    print("Lower: {:.2f}".format(v_lower))
    print("Upper: {:.2f}".format(v_upper))
    
    for index, row in df.iterrows():
        if row[col]<v_lower or row[col]>v_upper:
            df.loc[index, 'outlier'] = 'outlier'

    print("Number of outliers: {}".format(df[df.outlier == "outlier"].shape[0]))
    
    fig, ax = plt.subplots(figsize=(15, 15))
    sns.histplot(data=df, x=df[col], hue=df['outlier'], ax=ax)
    
    if save_histogram == True:
        fig.savefig("histogram/{}.png".format(col))
    else:
        plt.show()
    
    print(30*"-")

for feature in numeric_col:
    outlier_interquartileRangeMethod(df, feature, save_histogram=False)

The function has in total three attributes:

• df is the pandas DataFrame that contrains the dataset
• feature is the current feature where we want to calculate the outliers
• save_histogram is a variable that can be set to False to not save the distribution of the feature as png file but show the histogram in the Jupyter notebook, or True to save the distribution as png file.

Either if we save the histogram as file or show is only in the Jupyter Notebook, we print some values for each feature to the Jupyter Notebook to see the information that are the reason why a sample is declared as outlier or not.

In the first line of the function we print the current feature and only keep this feature from the dataset. Therefore we can not delete all missing values and create a second column called outlier where we first declare all samples as no outlier.

The first step to compute the 5-th and 95-th percentile from the current feature and print both values to the Jupyter console. Now we compute a new variable (v_iqr) that is the difference between the 95-th and 5-th percentile and therefore a measurement how wide or narrow the distribution of the feature is. You could also try to create a function that uses the variance of the distribution.

Now I multiply the variable v_iqr with a “safety factor” of 1.5 that you could also change dependent on your objective how fast you want to declare a sample as outlier. The new variable (v_cut_off) is now used to calculate the lower and upper threshold when a sample is declared as outlier. The lower band is calculated by substracting the cut off ratio from the 5-th percentile and the upper band is therefore calculated by adding the cut of ratio to the 95-th percentile. We print all these values also to the notebook output.

Now we can loop over all samples and compare the value of the sample with the lower and upper band. If the value is lower than the lower band or higher than the upper band, the sample is declared as outlier and the outlier column is changed. After we looped over all samples we count the total number of outliers and print the value to the output.

The last part of the function is to create a distribution plot and is separated by the outlier column. If the attribute save_histogram is true, the plot is saved to a new created folder or the plot is shown in the notebook output.

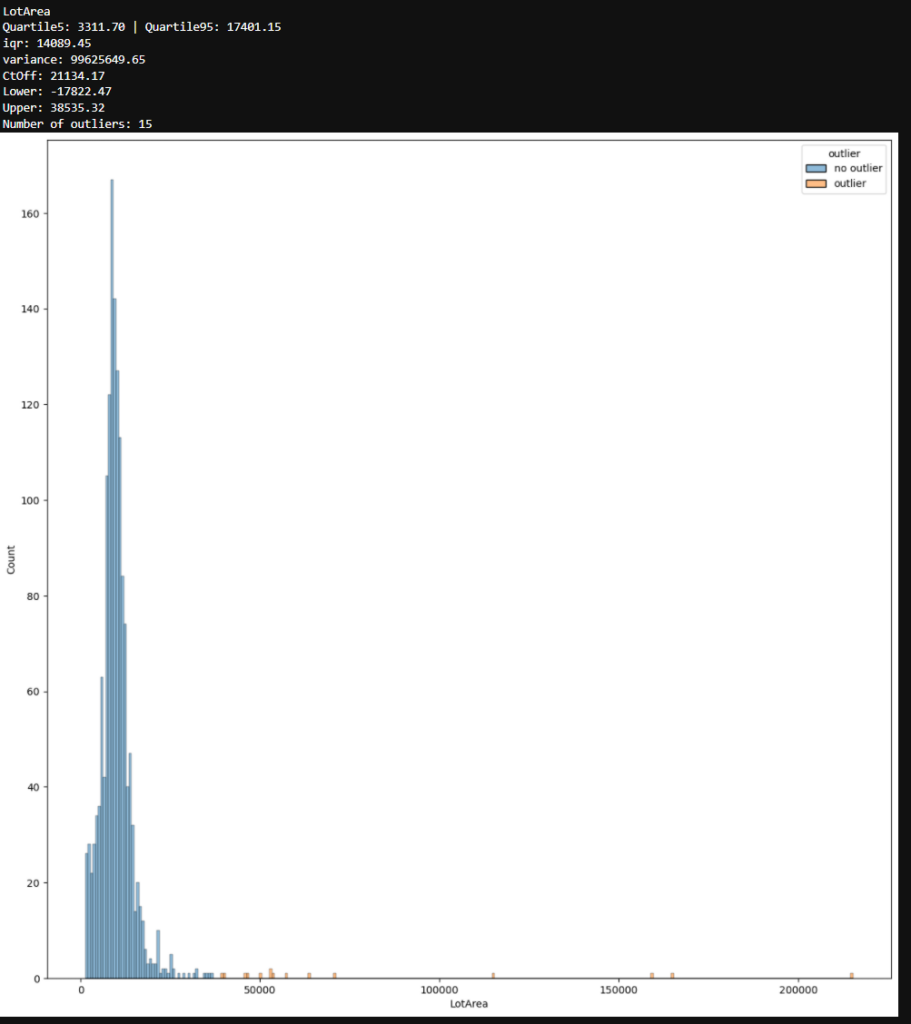
The following screenshot shows an example of one feature in the dataset that contains outliers after the interquartile range method.

Find Outlier and Create PDF Report

The second function create_outlier_interquartileRangeMethod_report computes the same numbers but creates also a PDF report from all the information that is printed to the notebook output and contains the distribution of every feature. For the creation of the PDF I use the PyFPDF library that you maybe have to first intall.

def create_outlier_interquartileRangeMethod_report(df, col):
    pdf.add_page()
    
    df = df[[col]].dropna(axis='index')
    df['outlier'] = 'no outlier'
    
    q5, q95 = np.percentile(df[col], 5), np.percentile(df[col], 95)
    v_iqr = q95-q5

    v_cut_off = v_iqr*1.5
    v_lower, v_upper = q5-v_cut_off, q95+v_cut_off
    
    for index, row in df.iterrows():
        if row[col]<v_lower or row[col]>v_upper:
            df.loc[index, 'outlier'] = 'outlier'

    if os.path.isfile("histogram/{}.png".format(col)):
        print("histogram for {} is already created".format(col))
    else:
        fig, ax = plt.subplots(figsize=(15, 15))
        sns.histplot(data=df, x=df[col], hue=df['outlier'], ax=ax)
        fig.savefig("histogram/{}.png".format(col))
            
    
    pdf.multi_cell(0, 5, "Quartile5: {:.2f} | Quartile95: {:.2f}".format(q5, q95))
    pdf.ln()
    pdf.multi_cell(0, 5, str(col))
    pdf.ln()
    pdf.multi_cell(0, 5, "CtOff: {:.2f}".format(v_cut_off))
    pdf.ln()
    pdf.multi_cell(0, 5, "Lower: {:.2f}".format(v_lower))
    pdf.ln()
    pdf.multi_cell(0, 5, "Upper: {:.2f}".format(v_upper))
    pdf.ln()
    pdf.multi_cell(0, 5, "Number of outliers: {}".format(df[df.outlier == "outlier"].shape[0]))
    pdf.ln()
    pdf.image("histogram/{}.png".format(col), x = None, y = None, w = 200, h = 150, type = '', link = '')


from fpdf import FPDF
pdf = FPDF()
pdf.set_font('Arial', 'B', 16)

for feature in numeric_col:
    create_outlier_interquartileRangeMethod_report(df, feature)
    
pdf.output('histogram.pdf', 'F')